Lunar Influences on the Reproductive Cycle in Women

By Winnifred B. Cutler 1,2,5, Wolfgang M. Schleidt 3, Erika Freidmann 4, George Preti 2, and Robert Stine 6
*This study replicated the 1980 paper published in the American Journal of Obstetrics and Gynecology; Lunar and Menstrual Phase Locking.
*Please click on bold print within text below for details and/or studies in full.
*Please click here for more on pheromones and books from Athena Institute
Copyright ©1987 Wayne State University Press,
Journal: HUMAN BIOLOGY December 1987, Volume 59 Number 6
Abstract:
Several exogenous influences on the human female's menstrual cycle length have recently been demonstrated. Previously, sexual behavior and pheromonal influences have been described. This report evaluates lunar cyclicity patterns.
A relationship is demonstrated between the onset of menstruation, among women who have 29.5 + 1 day menstrual cycles, and the onset of full moon. Four separate prospectively gathered sets of data are presented from different years and seasons. It is demonstrated that these women tend to menstruate in the full of the moon with a diminishing likelihood of menses onset as distance from full moon increases.
Introduction
The length of a woman's menstrual cycle has long been known to bear some reflection of the underlying endocrine milieu as well as her potential for fertility. Vollman at al. (1968, 1970, 1977) as well as Treloar et al. (1967, 1981) through their extensive prospective studies, have clearly shown that women whose cycles approach the 29.5 day span have the highest likelihood of fertile cycles, while women whose cycles become longer or shorter have a proportionately diminishing incidence of fertile cycles. About 28% of reproductively mature women show a 29.5 + 1 day cycle length (Vollman 1968, 1970, 1977).
That the most fertile reproductive cycle has the same length as the lunar cycle, i.e. 29.5 days, is an intriguing biological coincidence. In 1979, we reported that although previous investigators had failed to find a relationship between menses onset and the lunar cycle, their failure derived from the inappropriateness to the methods employed. By selecting the subpopulation of women (approximately 30%) who cycle as often as the moon does, i.e. 29.5+1 day, a significant pattern was revealed. There was an increased likelihood of menstruation onset in the light half of the lunar month. Thus, in a selected population of 312 women, prospective menstrual cycle records maintained during the Autumn of 1977 showed that 69% of the subsample whose menstrual length was 29.5+ 1 day showed menses onset within 7.5 days of the full moon (Cutler 1980a).
A year later, Friedmann (1981) replicated this phenomenon, reporting that 65% of a similarly sized population menstruated in the light half of the lunar cycle. In her sample, the split was optimized with a 3 day lag period after the quarter; i.e. the month was bisected 3 days after the first and third quarter.
In this report, we re-evaluate those data using a more sophisticated analytic method and we add data from prospective records collected during 2 other experiments. We hypothesize that a systematic relationship between day of the lunar cycle and density of menses onsets might exist. We also explore whether the season can influence these lunar, menstrual associations.
Dr. Cutler's pheromone science has been "bottled" into vials of unscented fragrance additives that increase wearers' sexual attractiveness. AVAILABLE FOR PURCHASE HERE
More recently, exogenous influences on menstrual cycle length and other reproductive endocrine patterns have been reported (Cutler et al. 1979a,b,c, 1980, 1983,1985,1986; McFalls 1973; McCoy et al. 1985). For example, women who engage in regular weekly heterosexual intercourse tend to have significantly more 29.5+3 day cycles, higher incidences of fertile patterns of basal body temperature graphs, and higher levels of circulating estrogen in both the reproductive and the climacteric years than women who have either celibate or sporadic patters of sexual behavior (Cutler et al. 1979a, b, 1980b, 1983,1985,1986a; McCoy et al. 1985). Through analyses of data trends, the direction of causality was considered to be behaviorally manipulable (Cutler et al. 1985,1986); regular weekly behavior appears sufficient to create 29.5+3 day cycles.
Investigation into the underlying mechanisms by which sexual behavior may affect the neuroendocrine rhythm of women has yielded evidence for a pheromonal influence (McClintock 1983, 1984; Cutler et al. 1984, 1986; Preti et al. 1986). Studies in our laboratories employing extracts of axillary secretions from donor men and donor women were shown to significantly alter the timing and length of menstrual cycles of nulliparous women in a double-blind, placebo-controlled study (Cutler et al. 1986; Preti et al. 1986, 1987). Consequently, there appear to be several exogenous influences which promote lunar type cycle lengths in women.
Materials and Methods
Collection of Menstrual Data
Calendars designed for convenient recording of menstrual and sexual events were employed in four subsequent studies (Cutler 1979 a, b). Each calendar contained 4 or 5 months of dated slots for individual days and was designed to fit within a wallet. Subjects prospectively gathered data for approximately 14 weeks. Details of the prospective double-blind methods of data collection are described elsewhere (Cutler 1979a). Briefly, subjects were told that they were participating in a study to increase our understanding about reproductive physiology of the menstrual cycle.
Sample and Analysis of Menstrual Calendars.
Table 1 indicates the number of women for whom menses data were collected in each sample, as well as the percentage of that sample who showed a 29.5 + 1 day cycle. Of all subjects, 27% had 29.5+ day cycles. In the 3 Philadelphia studies, only nulliparous, unmarried women participated. No one who used either oral contraceptives or IUD's was included. In addition, roommates were not permitted to enroll. Thus, only one subject per any combined dorm suite could be enrolled. Calendars were collected at the end of the experiment and the length of each menstrual cycle was calculated and recorded. Each calendar, with its several menses lengths, was then processed again to calculate the average (mean) and standard deviation in cycle length for each subject. All of those calendars with a mean cycle length of 29.5+ 1 day were selected and analyzed for the purpose of this report.
In order to avoid the problem of multiple, non-independent input of data which would spuriously expand on the effect we were evaluating, only one cycle onset per subject was tabulated in this report. For all of the Autumn analyses (1976, 1977, and 1979), the menses onset within the month of October was selected because it is a non-holiday month within the University setting. A tabulation was made to determine how many women had their menses onset on October 1, how many on October 2, October 3, October 4, and so on.
Size |
|||||||
|
|
|||||||
1976 |
127 |
40 |
31% |
||||
1977 |
312 |
68 |
22% |
||||
1979 |
305 |
97 |
32% |
||||
1983 |
Philadelphia | Senses Center |
94 ____ |
24 ____ |
26% ____ |
||
838 |
229 |
27% |
|||||
Menses Relationship to Moon Cycles.
An almanac was used to determine when the new moon had occurred. Once a histogram (frequency count) had been developed for each day in relation to the distance from the new moon (see Table 2) a kernel density analysis (as detailed below) was performed by computer. Thus, each day in October was converted into the "day since new moon" and each day of the lunar cycle could now be represented as to the frequency with which women with 29.5+1 day cycles began menstruation.
A random distribution would yield a flat density since it would be equally likely for women to begin to menstruate on any day of the lunar cycle. A departure from a straight line thus indicates non-randomness; i.e. whether there was a lunar effect on menstrual onset for these women. The significance of the lunar effect could then be tested.
Kernel Density Evaluation.
Histograms of lunar menses onset show clustering in that onsets tended to occur in proximity. A kernel density procedure delineates the clustering by smoothing these histograms as in Figures 1 through 4. A kernel density estimate produces a smooth curve which captures the underlying trends in a histogram by eliminating much of the random sampling variability. A kernel density estimate is similar to a weighted, centered moving average in that we average the frequencies of adjacent histogram categories. Unlike the constant weights used in a moving average , weights in a kernel density estimate are larger near the center than the extremes. For example, a three term moving average uses three equal weights of one-third to produce the running total. By comparison, a comparable kernel might combine more categories, but it concentrates the weights near the center, such as with the weights .05, .20, .50, .20, .05. Concentrating the weights in the middle helps avoid too much smoothing which can obscure important features in the data.
The density estimates in all figures utilize the kernel appearing in Silverman (1978) (the width parameter "h" from that paper was set to 7 days and was chosen using the test graph principle of Silverman). Smoothing at the "edges" of the x-axis is handled by viewing the data as if they were wrapping around a circle; the cells at the two ends of the histogram are treated as adjacent. The vertical scaling in the graphs is chosen so that the area under the curve is one. Hence, the probability of an onset within a give range on the x-axis is estimated by the area under that portion of the curve.
| Days since New Moon | Fall 1976 | Fall 1977 | Fall 1979 | Spring 1983 | ||
1 |
0 | 1 | 4 | 0 | ||
2 |
1 | 0 | 3 | 0 | ||
3 |
0 | 3 | 4 | 1 | ||
4 |
0 | 3 | 4 | 0 | ||
5 |
1 | 2 | 2 | 1 | ||
6 |
3 | 0 | 2 | 0 | ||
7 |
1 | 1 | 2 | 1 | ||
8 |
3 | 1 | 4 | 0 | ||
9 |
1 | 4 | 2 | 0 | ||
10 |
2 | 3 | 1 | 3 | ||
11 |
1 | 4 | 2 | 2 | ||
12 |
4 | 3 | 8 | 1 | ||
13 |
2 | 3 | 3 | 1 | ||
14 |
2 | 3 | 6 | 2 | ||
15 |
1 | 5 | 4 | 0 | ||
16 |
1 | 3 | 0 | 1 | ||
17 |
2 | 2 | 4 | 1 | ||
18 |
3 | 4 | 0 | 1 | ||
19 |
0 | 1 | 9 | 0 | ||
20 |
1 | 4 | 2 | 1 | ||
21 |
2 | 5 | 5 | 1 | ||
22 |
2 | 2 | 5 | 2 | ||
23 |
2 | 1 | 6 | 2 | ||
24 |
0 | 4 | 1 | 1 | ||
25 |
0 | 1 | 3 | 1 | ||
26 |
1 | 1 | 6 | 1 | ||
27 |
1 | 3 | 4 | 0 | ||
28 |
3 | 1 | 0 | 0 | ||
29 |
0 | 0 | 0 | 0 | ||
30 |
0 | 0 | 1 | 0 | ||
Standard Error Boundaries.
The standard error bounds which appear in all figures are produced using the bootstrap resampling procedure (Efron 1979, 1982). This resampling procedure yields an estimate of the sampling variation of a statistic by mimicking the original sampling process. The variation of a statistic arises because of sampling variation -- different random samples typically lead to different values of the statistic. To estimate such variability, we would ideally like to get more samples from the same population so that we could see how the statistic varies when calculated from the different samples. However, it is not usually possible to get such repeated samples, and one is tempted to resort to hypothetical sampling models.
Bootstrap resampling avoids this recourse to utopian assumptions about the sampling process and places more emphasis on the observed data. Rather than assume that the sample is from some hypothetical population, the bootstrap works by drawing repeated samples, with replacement, from the observed data. Thus, one "supposes" that the observed data set is the population and draws repeated samples (called "bootstrap samples") from it. To estimate the variation in the true population, one uses the variation in the statistic of interest across these bootstrap samples. The method has been shown to be very reliable in producing useful variance estimates for complex statistics, such as the kernel density estimates used here.
To apply the bootstrap, 50 samples with replacement from the original sample were drawn. Each bootstrap sample yields a histogram which is smoothed with the kernel density procedure. A collection of 50 kernel density estimates are obtained and averaged across replications to yield an average density estimate. The standard deviation across the 50 kernel estimates is computed in similar fashion which provides the standard error bounds shown in the figures.
Though the bootstrap standard error bounds appear rather small, the available sample sizes are typically small.
| Table 3. Significance Levels of Comparisons of the Observed Onset Distributions to a Uniform Distribution (Diagonal) and Each Other (Off-Diagonal) |
|||||
|
|
|
|
|
|
|
|
|
|||||
|
Fall 76 |
|
|
|
|
|
|
Fall 77 |
|
|
|
|
|
|
Fall 79 |
|
|
|
||
|
Spring 83 |
|
|
|||
|
|
|||||
| Comparisons to the uniform are based on the Vn staticstic of Stephens (1965) and the comparisons between samples are based on the Vnm test of Stephens (1965) and Maag (1968) NSD= no significant difference | |||||
Results
Two statistical questions are raised:
1) Does any graph differ significantly from a uniform distribution? and
2) Which figures are significantly different from each other?
Table 3 addresses both questions. On the diagonal appears the answer to question #1. All other points reflect question #2.
Table 3 shows, on its diagonal, that both the lunar/menstrual distribution of Fall of 1977 and 1979 are significantly different from non-random distributions.
Figure 1 shows the kernel density evaluation of the Autumn 1976 sample. One notes a visually apparent variation in menses onsets. Figure 2 appears to be similar in character. For example, in the data of Fall 1977, most onsets occur about 15 days after the new moon, i.e. at the full moon. Due to small sample sizes, only the histograms from Fall 1977 and Fall 1979
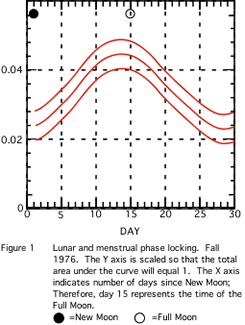
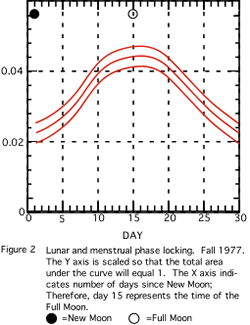
(Figures 2 and 3) differ significantly (p=0.05) from a uniform distribution on the circle (see Table 3). The other samples are considered as indicative of what might have occurred if we had gathered larger samples.
Figure 3 shows the New York sample and reveals a similar pattern to the 1976 and 1977 data arrays with perhaps a phase shift in the peak occurring 2 days after the full moon.
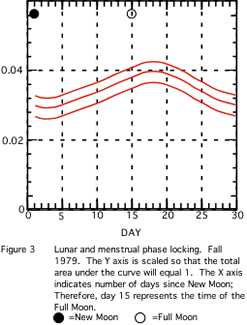
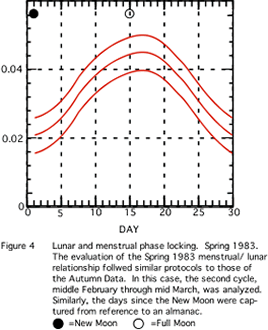
A visual inspection of Figure 4 (Spring 1983) reveals a similar character to the data array.
Conclusions
This study shows a relationship between the changing phases of the moon and the propensity for menstrual onset in women. This phenomenon was demonstrated in the subset of 229 women who cycle as often as the moon cycles. Cutler's earlier report (1980a) had shown that data of non-29.5+1 day cyclers distributed randomly about the lunar month.
This was expected from mathematical considerations when one realizes the nature of the cycles. For example, if the lunar cycle were drawn as a clock that had 30 (rounded up from 29.5) "pie sectors", and a particular woman who did not have a 29.5 day cycle was charting her data, certain phenomena would emerge. As an example, consider a women who menstruates on a regular 35 day cycle. If she plotted 6 cycles of her own on the 30 day clock, and the first cycle appeared at the full moon, then the next cycle would appear 5 days after the full moon and the third cycle would be 5 days later than, and so on.
Thus, a woman who has a regular 35 day cycle would eventually distribute her onsets completely around the clock and fail to show any lunar relationship. Similar considerations occur when we chart cross-sectional data of women with non-29.5 day cycles. One would expect a rather random distribution around the clock.
It is noteworthy that a number of studies have shown that the 29.5+ 1 day lunar cycle is coincident with the most fertile menstrual cycle (Vollman 1968, 1970, 1977; Treloar et al. 1967)
In the 4 separate studies of women living naturally, visual inspection of the figures (1 through 4) suggests a common phenomenon: the highest density in every case appears to be at about the full moon: that is 15 or so days after the new moon. The small Spring sample does not appear to differ from these Autumn samples, suggesting no seasonal effect. Although only Figures 2 and 3 contain sufficiently large samples for statistically significant difference from a non-uniform distribution, the similarity in graphs is noteworthy.
The menstrual life of a woman is known to pass through three phases: 1) the pubescent occupying the first 7 years after menarche; 2) the reproductive years; and 3) the premenopausal occupying the last 7 years before menstruation ceases (Cutler and Garcia 1984). It is during the reproductive years of women that the 29.5+1 day cycle most commonly occurs and in larger scale studies, an incidence of approximately 32% is obtained (Vollman 1977). Thus, it is during the reproductive years (approximately age 20 through 42) when this lunar influence would be testable.
It is not surprising to learn of a coordinated phase relationship between the reproductive cycles of women and the repeating cycle of lunar periods because even a cursory review of the literature shows that many different animals show a reproductive system reaction to external stimuli. Exogenous influences on the fertility of organisms have been demonstrated in several species with respect to geophysically ordered time. A seasonal variation in human birth rate has been documented with troughs in Spring and peaks in Autumn (Rosenberg 1966; Pasamanick et al. 1959). Coordinated phase relationships between reproductive rhythms and lunar rhythms are documented in monkeys, genus Cercopithecus (Reiter 1972) as well as in the fiddler crabs (Brown et al. 1953). Persistent activity rhythms that are coordinated with lunar rhythms have been well documented in a variety of organisms including the frog, Rana pipiens (Robertson 1978), the crab Carcinus maenas (Naylor 1958, 1960), the marine worm Platynereis (Havenschild 1960), the hamster (Brown 1967), and planarians (Brown et al. 1975).
The demonstration that women who cycle as often as the moon tend to be the most fertile and that among these women there is an increased propensity for menstruation at or about the full moon is particularly noteworthy. Historical indication that fertility rites were scheduled with consideration for the phase of the moon may have been reflecting accurate perceptions which we have yet to discover.
Received June 1986; revision received 17 February 1987.
References and Citations
Author affiliations (at time of publication)
1.Athena Institute for Women's Wellness
2.Monell Chemical Senses Center
3.Osterreichische Academie der Wissenshaften, Institut für Vergleichends Verhaltensforchung, Vienna.
4.School of Science, Department of Health Science, Brooklyn college of CUNY, Brooklyn, New York.
5.Department of Obstetrics and Gynecology, University of Pennsylvania, Hospital of the University of Pennsylvania, Philadelphia, PA 19104.
6.University of Pennsylvania, Statistics Department, Wharton School, Philadelphia, PA
Literature Cited
Brown, F.A., M. Fingerman, H.M. Webb and M.I. Sandeen 1953 Persistent diurnal and tidal rhythms of color change in the fiddler crab Uca pugnax. J. Exp. Zool 123:29-52.
Brown, F.A. and Y.H. Park 1967 Synodic Monthly modulation of the diurnal rhythm of hamsters. Proc. Soc. Expr. Biol. and Med. 25:712
Brown, F.A. and Y.H. Park 1975 A persistent monthly variation in responses of planaraians to lights, and its annual modulation. Internat. J. Chronobiology, 3:57-62
Cutler, W.B., C.R. Garcia and A.M. Krieger 1979a Sexual behavior frequency and menstrual cycle length in mature premenopausal women. Psychoneuroendocrinology, 4:297-309
Cutler, W.B., C.R. Garcia and A.M. Krieger 1979b Luteal phase defects: A possible relationship between short hyperthermic phase and sporadic sexual behavior in women. Hormones and Behavior, 13:214-218
Cutler, W.B., C.R. Garcia and A.M. Krieger 1979c Infertility and age at first coitus: A possible association. J. Biosoc. Sci. 11:425-432
Cutler, W.B., 1980a Lunar and menstrual phase locking. Am.J. Obstet. Gynecol. 137:834-839
Cutler, W.B., C.R. Garcia and A.M. Krieger 1980b Sporadic sexual behavior and menstrual cycle length in women. Hormones and Behavior, 14:163-172
Cutler, W.B., N. MCCoy and J.M. Davidson 1983 Steroids and hot flashes are associated during the perimenopause. Neuroendo. L. 5:185
Cutler, W.B. and C.R. Garcia 1984 Medical Management of Menopause and Premenopause:Their Endocrinologic Basis. J.B. Lippincott, Philadelphia, PA.
Cutler, W.B., G. Preti, W.B. Huggins, G. Preti, G.R. Huggins, B. Erickson and C.R. Garcia 1985 Sexual behavior frequency and biphasic ovulatory type menstrual cycles. Physiol. Behav. 34:805 810
Cutler, W.B., C.R. Garcia, G. Huggins and G. Preti 1986a Sexual behavior and steroid levels among gynecologically mature premenopausal women. Fertil. Steril. 45:496-502
Cutler, W.B., G. Preti, A.M. Krieger, G. Huggins, C.R. Garcia and H.J. Lawley 1986 Human Axillary Secretions Influence Women's Menstrual Cycles: The Role of Donor Extract from Men. Hormones and Behavior, 20:463-473
Efron B. 1979 Bootstrap methods: Another look at the jack-knife. Biometrika, 65:1-26
Efron, B. 1982 The Jackknife, the bootstrap, and other re-sampling plans. Society for Industrial and Applied Mathematics, Monograph No. 38, Philadelphia.
Friedmann, E. 1981 Menstrual and lunar cycles. Am. J. Obstet. Gynecol. 140:350
Havenschild 1960 Lunar Periodicity. Cold Spr. Harb. Symp. Quant. Biol. 25-491:497
Maag, R. and M. A. Stevens 1968 The vnm two-sample test. Annals of Math. Statistics, 39:9;23-935
McClintock, M.K. 1983 Pheromonal regulation of the ovarian cycle: Enhancement, suppression and synchrony. In Pheromones and Reproduction in Mammals J.G. Vandenbergh (ed) Academic Press, NY pp. 113-149
McClintock, M.K. 1984 Estrous synchrony: Modulation of ovarian cycle length by female pheromones. Physiology and Behavior, 32:701-705
McCoy, N., W.B. Cutler and J.M. Davidson 1985 Relationships among sexual behavior, hot flashes, and hormone levels in perimenopausal women. Arch. Sex. Behav. 14:385-394.
McFalls, J.A. Jr. 1973 Impact of VD on the fertility of the US Black population, 1880-1950 Social Biology, 20:2-19
Naylor, E. 1958 Tidal and diurnal rhythms of locomotory activity in carcinus maenas (L) J. Exp. Biol. 35:602-610
Naylor, E. 1960 Locomotory rhythms in Carcinus Maenas (L) from noon tidal conditions. J. Exp. Biol. 37:481-488
Pasamanick, B. S. Dinitz and H. Knoblock 1959 Geographical and seasonal variations in birth rates. Pub. Health Reports, 74:285-288
Preti, G., W.B. Cutler, C.M. Christensen, H.J. Lawley, G. Huggins and C.R. Garcia 1987 Human Axillary Extracts: An Analysis of Compounds from Samples Which Influence Menstrual Timing. J. Chem Ecol. (in Press)
Preti, G., W.B. Cutler, A.Kreiger, G. Huggins, C.R. Garcia and H.J. Lawley 1986 Human Axillary Secretions Influence Women's Menstrual Cycles:The role of donor extract from women. Hormones and Behavior 20:474-482
Reiter, R.J. 1972 The role of the pineal in reproduction. In: Balin, H. and S. Glass (eds.) Reproductive Biology. Excerpta Medica, New York.
Robertson, D.R. 1978 The light-dark cycle and nonlinear analysis of lunar perturbations and barometric pressure associated with the annual locomotor activity of the frog Rana pipiens. Biol. Bull. 154:302-321
Rosenberg, H.M. 1966 Seasonal variations of births. United States 1933-63. US. Dept. of Health Education and Welfare PHS Publ. 1000, series 21, No. 9.
Silverman, B.W. 1978 Choosing the window width when estimating a density. Biometrika, 65:1-11
Stephens, M.A., 1965 The goodness-of-fit statistic Vn: Distribution and significance points. Biometrika, 52:309-321
Treloar, A.E., R.E. Boynton, D.G. Behn and B.W. Brown 1967 Variations of the human menstrual cycle through reproductive life. Int. J. Fertil. 12:777-126
Treloar, A.E. 1981 Menstrual cyclicity and the premenopause. Maturitas. 3:249-264
Vollman, R.F. 1968 The length of premenstrual phase by age of women. In: Proceedings of the Fifth World Congress on Fertility and Sterility, Stockholm, Amsterdam, Excerpta Medica International Congress Series No.133 pp.1171-1175
Vollman, R.F. 1970 Conception rates by days of the menstrual cycles, BBT, and outcome of pregnancy. Sixth World Congress of Gynecology and Obstetrics of the International Federation of Gynecology and Obstetrics, New York, Abstracts, Williams and Wilkins, Baltimore No.112
Vollman R.F. 1977 The Menstrual Cycle. In: Major Problems of Obstetrics and Gynecology. W.B. Saunders, Philadelphia.
" My research has consistently focused on what behavior a woman can engage in to increase her power, well-being, and vitality."
---Winnifred B. Cutler, Ph.D.
A portion of the profits from our book and pheromone sales helps to fund Athena's on-going research.